Ark is a design to scale payments on Bitcoin. There are several explanations out there about Ark, but I couldn’t understand most of them, so I wrote my own. I also summarize how different opcode soft forks can help improve Ark properties, and compare Ark with other designs to address scalability like Lightning and rollups.

Motivation

Imagine you want to enable many users to share an on-chain UTXO, making payments with little on-chain footprint. You also want to do this in a non-custodial manner, so each user should be able to unilaterally exit from the shared UTXO to their own on-chain UTXO any time they want.

Why might you want this? Well, Lightning lets you make off-chain payments non-custodially, but it has some issues around liquidity and it still requires a UTXO per user. If successful, the UTXO set size on Bitcon nodes will be a constraint in the future: all validating nodes need to store the UTXO set in order to validate transactions. Right now there are ~170M UTXOs and the serialized size of the UTXO set is ~11GiB. Back-of-the-envelope if every person in the world had just one UTXO, the serialized size of the UTXO set size would grow to be half a terabyte, which is not awesome for something on the critical path for validation.¹

There have been designs proposing how users might share UTXOs, like coinpools, but they require all users to be online to sign to change the balances in the coinpool. Ark makes it so not all users have to be online to sign if a user wants to enter or exit the pool, or if they want to change the balances in the pool. It does so by using multiple shared UTXOs (over rounds, and in transaction trees) and creating a role for a privileged operator, S. This design enables many scalable payments by having many users working together with the same S. If S cooperates, many users can make many payments to each other in the pool, batched into only a single, small on-chain transaction every round. Even if S doesn’t cooperate, the users can exit to their own on-chain UTXO without S’s permission (assuming they can pay the appropriate fees to do so).

However, there are a few stipulations to this:

1. Like Lightning, there is an added liveness requirement; users need to come online every so often or they might relinquish their funds. This period can be set to a while, like a month. We call this the refresh period.

2. Exiting on-chain might be more expensive for the user than even a simple on-chain payment transaction, because it actually requires multiple on-chain transactions. We hope this doesn’t happen much and instead most payments are made cooperatively in the pool.

3. To exit non-cooperatively, the user needs to have enough UTXOs lying around to pay the fees to get their transactions onchain

4. S needs to be online and provide extra liquidity (in the amount of the payment volume) for as long as the refresh period. So there is a trade-off: a shorter refresh period is better for liquidity costs to the server (and thus, presumably, Ark fees which get passed on to users) but this means users have to come online more often.

S does not sequence a rollup—there is no state machine of payments in an execution of the protocol. Instead, S creates commitments to trees of exit transactions by posting the root of each tree (a shared UTXO) every so often, in rounds. One way this is unlike a rollup is because previous trees might still have valid exit paths for users.

There are many variants of Ark with different trade-offs. I describe one here, then describe another if you add CTV, which reduces interactivity, and then another with CTV and CSFS, which helps interactivity even more.²

Ark protocol

There is an Ark operator S and users A, B, C, … The pool, or Ark, has the following operations: Join, Transfer, Refresh, Exit. Users join the Ark by spending to a special transaction with S, and pay each other by interacting with S. S posts commitments to different transaction trees on-chain, and users hold off-chain transactions to unilaterally exit the Ark. Exiting can be cooperative or non-cooperative (based on S). Everything described here will maintain the following properties: 1) users don’t trust S with custody; they can always exit with their funds within the refresh period and 2) S doesn’t rely on users to get its money out eventually.

This description does not discuss what are sometimes called “Arkoor” or “out of round” payments, which have lower latency but require the recipient of a payment to assume S and the spender don’t collude. We are making no such assumptions here (this also originally confused me; I thought Ark required this assumption for any payment, making the threat model more like statechains. It does not). This means that unlike Lightning, Ark payments are pretty high latency.

I use bold to indicate Bitcoin transactions, that might be broadcast and confirmed, or might be held off chain. There are four main types of transactions: join, exit, forfeit, and round.

Joining the Ark

Alice joins the Ark by spending some of her coins to S in the following way: she asks S to co-sign an exit transaction and posts a join transaction on-chain. It works as follows: A uses her own UTXO as input (let’s say 7 BTC). The join transaction has an output with a clause requiring a signature from both A and S, which we shorthand as (A+S). Off-chain, Alice keeps an exit transaction taking this output as input and spending to the following clause: (A+S or A w/ \(\delta\)). Alice asks S to sign exit, then signs and posts join on-chain. See here for Second Lab’s figure showing the transactions (they call join “Onboard”):

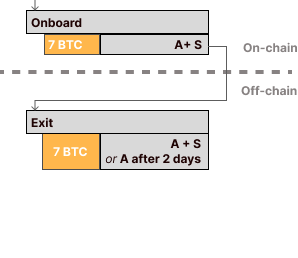
The first time threshold is a relative time, \(\delta\), using CSV. This is the time a user has to wait until they can get their money out of the Ark if S doesn’t cooperate. This is also the time in which S needs to come online in order to sweep forfeit transactions, which we’ll describe later. In the picture above, this is two days.

Once join has confirmed, Alice has joined S’s Ark and can make cheap payments:

• S knows that join can only be otherwise spent by the exit transaction described above (because of the multisig in join).
• Alice knows she can always broadcast the S-signed exit transaction to exit the Ark and issue another transaction getting her money back in \(\delta\) time.

Ark rounds

We’ll add two more times:

An expiry time, \(\Delta\). This is the required refresh period, and the amount of time S has to front liquidity for payments. After this time, S can sweep any outstanding round transactions or trees (described later). This is an absolute time, usually set to something like a month in the future. A user who has made payments needs to come back online within this time and either Transfer, Refresh, or Exit in order to prevent their money from being taken.

A round time. This is the time between on-chain round transactions by S, which ensure commitment of user payments or refreshes. This is one component of the user-perceived latency for transactions. This should be a lot less than the refresh period (maybe an hour or a day). It is not present as relative or absolute time locks in script, so I don’t bother giving it a variable.

Every round time, S makes a new on-chain transaction round handling and batching any Transfer, Refresh, and Exit operations. round commits to a new tree with the appropriate exit transactions.

If nothing happens besides Alice joining the Ark, then there don’t need to be any round transactions. Alice is in S’s Ark by herself. Let’s say Bob also joins S’s Ark with 1 BTC, and Alice wants to pay Bob.

Payments

Alice and Bob are already in an Ark, Alice with 7 BTC and Bob 1 BTC, and Alice wants to pay Bob .5 BTC.

1. Alice and Bob agree to terms for some sort of payment, and Bob shares his public key with Alice.

2. Alice tells S about this request for payment, sharing her and Bob’s public keys

3. Time passes. S waits until it is ready to make the next round transaction, collecting many of these requests into a batch

4. Once ready, S creates a new round transaction, the structure of which is described below. S needs to include its own new inputs to fully fund this transaction.

5. S shows the relevant branches of the transaction tree to Alice and Bob (and every user in this batch), and asks Alice and Bob (and each user) to sign the appropriate transactions in their branch of the tree and forfeit transactions (described below). These forfeits apply to the exit transactions Alice and Bob have for their respective 7 BTC and 1 BTC in the Ark, from previous joins (or rounds).

6. Once S received all appropriate signatures, S broadcasts the root transaction round to get it confirmed in a Bitcoin block, keeping the rest of the tree off chain.

7. round’s confirmation is the commit point for Alice’s payment to Bob – at this point Alice no longer has 7 BTC in the Ark, she has 6.5 BTC, and Bob no longer has 1 BTC—he has 1.5 BTC.

Round transaction tree and forfeits

round is a transaction with inputs supplied by S and two outputs, each a shared UTXO, with one output committing to the left side of the transaction tree and one committing to the right (you could imagine a k-way tree with k outputs instead of a binary tree). Each shared UTXO output’s clause is of the form (u+v+w…+S or S after \(\Delta\)) for the users in that shared UTXO, dividing the users in half (or by k) each level down. There is a leaf output in the tree for each user u whose balance has changed or who is refreshing in this round. Each leaf output has clause (u+S or S after \(\Delta\)), and an exit transaction which spends this output; recall, for a user like Alice her exit is a transaction spending to an output with a clause (A+S or A w/ \(\delta\)).

See this picture from Second Lab’s documentation for a visualization of a tree with users A, B, C, and D and 10 BTC.³

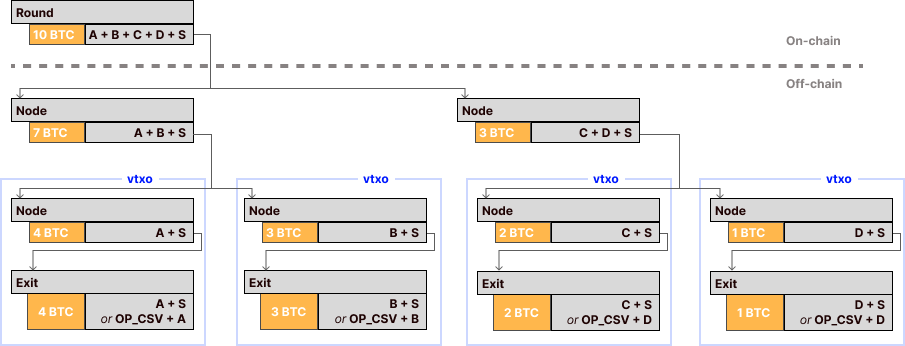
A forfeit transaction essentially cancels a user’s exit path in a round. It spends from the multisig clause of the exit transaction in the previous relevant round, to S, with no delays.

There is also a Refresh operation so a user can reset their expiry time. This is just like a user is making a payment to themselves. They relinquish their exit path in the previous (soon to expire) round transaction, and get a new one in a round transaction that expires later.

Atomicity

What I’ve described above is actually not safe.

Once S has a signed forfeit transaction from Alice, it could just never put the new round on chain, and it could broadcast the forfeit if Alice tries to exit a previous round, taking her money. This means Alice has no way to unilaterally exit! What we want is for forfeit to only be valid if the new round is on chain. This is done using connector outputs: Each forfeit should take as an additional input a dust-value output that is only created in the new round. So we add a bunch of connector outputs to the round transaction (one per forfeit).

Once a round transaction is on-chain, S has what it needs (connector outputs) to complete the input set for signed forfeits it holds from Transfers, Refreshes, and Exits from previous rounds, and it has effectively “canceled” those exit transactions.

A few things to note here:

First, annoyingly, Alice and Bob have to wait for a while between when they ask to make a payment until the transaction tree is actually constructed, and they need to be back online later right before the round is broadcast in order to sign the tree and forfeit, and give the signatures to S. Not only is it pretty interactive to make a payment, the users have to be online for the whole duration of the round. And to get the most batching benefit, S probably wants to wait a while to collect as many payments as possible. So users need to be online for a while.

Second, as you might have noticed, if even one user doesn’t show up to sign, S has to reconstruct the transaction tree for round to leave them out and get new signatures from everyone else. This is pretty bad, just one user each round can keep S from making progress. CTV helps by making it so only the spenders have to be online, and CTV+CSFS help remove this requirement entirely.

Exiting the Ark

To cooperatively exit, a user signs a forfeit depending upon an output paying them in the next round instead of a connector output.

To non-cooperatively exit, a user broadcasts the transactions that have not yet been confirmed in the path from their relevant transaction tree root round to their exit transaction. They might have to add fees. Some of these transactions might already be on chain if other users have exited. They will also have to wait a relative amount of time from when the exit is confirmed (\(\delta\)) to then spend the output. What prevents a user from broadcasting an old, out of date exit path? This \(\delta\) and the forfeit transaction! If a user broadcasts an old exit path, they will have to wait \(\delta\) for the clause where they can unilaterally spend the funds. S can immediately broadcast the relevant forfeit transaction and claim the output, without waiting \(\delta\).

In most of the articles describing Ark, they call the exit (and the path to it from round) a VTXO, or Virtual UTXO, and say a user “holds” VTXOs. I find this sort of confusing, honestly, because in the optimistic case a user doesn’t really spend their VTXOs the way they do actual UTXOs in transactions. Instead they forfeit them and get new ones.

S sweeping funds

S can immediately get all of the money it fronted for a round back in one transaction after \(\Delta\) (spending back to itself), as long as there have been no non-cooperative exits. If even one user has exited the round non-cooperatively (broadcasting their exit path on-chain) then S can only get the non-exited funds back, by opening up the rest of the transaction tree and putting siblings on-chain.

Adding Assumptions for Better Properties

CTV

If we had CTV, we can replace the multisigs with CTVs for the child transactions. This changes interactivity in the following places:

• Joining the Ark: Alice doesn’t have to get S to co-sign the exit, A+S in join can be a CTV to exit

• Users don’t have to sign the relevant paths in the transaction tree, but it doesn’t help interactivity that much because they still have to get the paths from S (after it has constructed the whole tree) before signing their forfeit transactions.⁴

• One could do an Ark variant where Bob, the recipient, does not need to be online to receive a payment, because he doesn’t have to be in the multisig. Bob shouldn’t consider the payment complete (release any goods to Alice) until he knows he can exit the Ark: He needs to know about the structure of round and have the appropriate exit transaction for himself, but he doesn’t need to acknowledge anything to securely commit the payment. We change the steps from before as follows:

Reminder, Alice and Bob are already in an Ark, Alice with 7 BTC and Bob 1 BTC, and Alice wants to pay Bob .5 BTC.

1. Alice and Bob agree to terms for the payment, and Bob shares his public key with Alice. This could happen at any point in the past, and then Bob can go offline.

2. Alice tells S about this request for payment, sharing her and Bob’s public keys.

3. Time passes. S waits until it is ready to make the next round transaction, collecting many of these requests into a batch

4. Once ready, S creates a new round transaction. S needs to include its own new inputs to fully fund this transaction.

5. S shows the relevant branches of the transaction tree to Alice (and every spender in this batch), and asks Alice (and each spender) to sign a forfeit transaction (they don’t have to sign anything in the branches because of CTV). Alice’s forfeit applies to the exit transaction Alice has for her 7 BTC in the Ark. THIS IS DIFFERENT FROM BEFORE: Bob is not going to forfeit his previous 1 BTC balance. He is going to keep that, and gain a new exit path for an incremental 0.5 BTC that Alice is paying him. Because he doesn’t forfeit anything he doesn’t need to be online for this part.

6. Once S receives all appropriate signatures, S broadcasts the root transaction round to get it confirmed in a Bitcoin block, keeping the rest of the tree off chain. round’s confirmation is the commit point for Alice’s payment to Bob—at this point Alice no longer has 7 BTC in the Ark, she has 6.5 BTC.

7. Bob shouldn’t release the goods to Alice until Alice both points to this transaction on chain and shares with him his branch (exit path) to his additional 0.5 BTC in the Ark.

Note that this is nicer than before because Bob doesn’t have to be online to get paid, and we’ve removed the recipients from the set of users who can keep a round from progressing (by not showing up at the end of the round to sign forfeit transactions).

CTV and CSFS

Adding CTV and CSFS enables rebindable signatures, which one can use to implement a variation called Erk. The general idea is that it’s safe for users to sign a variation on the forfeit transaction (called refund transactions in that post) before seeing the transaction tree because they know they’ll get paid back one way or the other. This changes the interactivity requirements a lot—users don’t have to stick around for the duration of the round.

Assuming S and the spender don’t collude

This enables Ark out-of-round, or Arkoor transactions, which are “instant”. I’m not interested in this assumption so I’m not going to go into detail on how this works, you can read about them here.

Note that Second Labs currently only implements Arkoor transactions for payments. If you don’t want to add this assumption as a recipient, you should come online and refresh in the next round before you consider yourself paid. I originally thought this was a bigger deal than it is; it’s really just an implementation detail.

How Ark compares

Lightning

Benefits of Ark:

• A really nice property of Ark is that Bob doesn’t need to have any liquidity in order to receive a payment! In contrast, in Lightning, if Bob doesn’t already have a funded channel, someone would need to front Bob liquidity to create a payment channel where Bob can receive.

• Another nice property is that Bob doesn’t have to be online to receive a payment (in the CTV variant). He just needs to come online before the refresh period.

• Another nice property of Ark is that we don’t have to worry at all about channel balances and routing. All that complexity goes away. This means I’d expect to see a much higher rate of successful payments in Ark than in Lightning.

Benefits of Lightning:

• In Lightning, if you can’t come online in time but you’ve only been spending, you’re fine (all previous states show you having more money than the current state). In Ark, if you can’t come online in time you could lose all your money.

• Ark doesn’t have the same low latency as Lightning with the same security assumptions.

• Unlike Lightning, Bob and Alice cannot transact peer-to-peer. They require S’s cooperation to make an off-chain payment. It’s kind of like if all users in an Ark are connected through a single Lightning hub, and not with each other.

Incomparable:

• The more users in an Ark, the more likely a payment can be satisfied off-chain, and the better scalability improvement. These payments have no additional on-chain footprint! But more users in one Ark probably makes it more likely a user might fail and S has to recompute a round.

Also something important to note is that it seems like designs for multiparty channels in Lightning (another way for multiple users to share a UTXO) are sort of “running into” incremental design changes to Ark. One way to think of this is imagine that the round transaction tree in Ark contained Lightning channel opens at the leaves. This is interesting and I’d like to understand this better but thus far I find the Lightning multi-party channels designs inscrutable.

Rollups on Bitcoin

This is a lot fuzzier to me because I haven’t read detailed rollup designs yet. Future post. Here are some speculative thoughts:

Benefits of Ark:

• Ark has way less data posted on-chain – rollup on-chain data is proportional to off-chain payments (specifically, state diffs). Ark and Lightning on-chain data are not.

• Ark doesn’t require a soft fork to be fully non-custodial. But without a soft fork it requires interactivity with all the users who are transferring, refreshing, or exiting every round (not all the users in the Ark, at least)

Benefits of rollups:

• Less interactivity. The rollup operator doesn’t have to talk to all the users making payments multiple times to get them to sign things.

• Rollups can have a totally different transaction model and virtual machine, so they can offer new functionality like privacy-preserving payments (zkCoins) or smart contracts.

• Ark relies on users to hold their exit paths (if they lose this data, then they can’t exit the Ark non-cooperatively). Bitcoin rollups pay higher on-chain storage costs so users don’t have to do this.

Not sure / TBD:

• Non-cooperative exit costs, and how this amortizes across users. In Ark if S totally fails multiple transaction trees need to go on-chain so users can exit. Not sure what happens if in a (non-custodial, so assume a future with CAT) rollup the sequencer fails (current rollups have a one-honest-operator requirement and cannot tolerate all operators failing)—since all data is on-chain, presumably someone else could just step in? Also, rollups can be designed so that if a challenger is doing an “honest” non-cooperative exit, the operator has to pay the on-chain assertion costs. But still, it takes up chain space, and I’m not clear on how much that is compared to Ark trees.

• I’d like to better understand the liquidity requirements of S in Ark vs. the rollup operators. Not entirely clear on that. Also unclear to me how the liquidity needs might be split between multiple operators.

Acknowledgements

Thanks to Antoine Poinsot for very helpfully whiteboarding Ark with me, Greg Sanders for explaining Ark in a Bitcoin scalability working group, and Antoine Poinsot, Jose Storopoli, Ethan Heilman, and Armin Sabouri for feedback on this post (no endorsement implied). All mistakes are my own.

References I found helpful:

• https://gist.github.com/RubenSomsen/a394beb1dea9e47e981216768e007454
• https://docs.second.tech/protocol/intro/
• https://delvingbitcoin.org/t/the-ark-case-for-ctv/1528
• https://delvingbitcoin.org/t/evolving-the-ark-protocol-using-ctv-and-csfs/1602

Footnotes